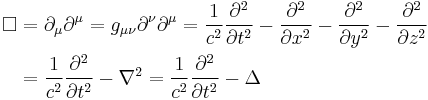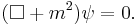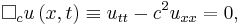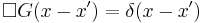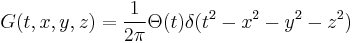D'Alembert operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator (represented by a box:  ), also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert. In Minkowski space in standard coordinates (t, x, y, z) it has the form:
), also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert. In Minkowski space in standard coordinates (t, x, y, z) it has the form:
Here 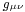 is the Minkowski metric with
is the Minkowski metric with 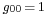 ,
, 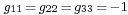 ,
, 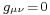 for
for 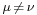 . Note that the μ and ν summation indices range from 0 to 3: see Einstein notation. We have assumed units such that the speed of light
. Note that the μ and ν summation indices range from 0 to 3: see Einstein notation. We have assumed units such that the speed of light 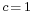 . Some authors also use the negative metric signature of [− + + +] with
. Some authors also use the negative metric signature of [− + + +] with 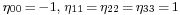 .
.
Lorentz transformations leave the Minkowski metric invariant, so the d'Alembertian is a Lorentz scalar. The above coordinate expressions remain valid for the standard coordinates in every inertial frame.
Contents |
Alternate notations
There are a variety of notations for the d'Alembertian. The most common is the symbol  : the four sides of the box representing the four dimensions of space-time and the
: the four sides of the box representing the four dimensions of space-time and the 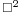 which emphasizes the scalar property through the squared term (much like the Laplacian). This symbol is sometimes called the quabla (cf. nabla symbol). In keeping with the triangular notation for the Laplacian sometimes
which emphasizes the scalar property through the squared term (much like the Laplacian). This symbol is sometimes called the quabla (cf. nabla symbol). In keeping with the triangular notation for the Laplacian sometimes 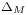 is used.
is used.
Another way to write the d'Alembertian in flat standard coordinates is 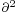 . This notation is used extensively in quantum field theory where partial derivatives are usually indexed: so the lack of an index with the squared partial derivative signals the presence of the D'Alembertian.
. This notation is used extensively in quantum field theory where partial derivatives are usually indexed: so the lack of an index with the squared partial derivative signals the presence of the D'Alembertian.
Sometimes  is used to represent the four-dimensional Levi-Civita covariant derivative. The symbol
is used to represent the four-dimensional Levi-Civita covariant derivative. The symbol 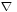 is then used to represent the space derivatives, but this is coordinate chart dependent.
is then used to represent the space derivatives, but this is coordinate chart dependent.
Applications
The Klein–Gordon equation has the form
The wave equation for the electromagnetic field in vacuum is
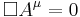
- where
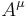 is the electromagnetic four-potential.
is the electromagnetic four-potential.
The wave equation for small vibrations is of the form
- where
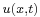 is the displacement.
is the displacement.
Green's function
The Green's function 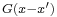 for the d'Alembertian is defined by the equation
for the d'Alembertian is defined by the equation
where 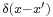 is the Dirac delta function and
is the Dirac delta function and 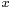 and
and 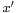 are two points in Minkowski space.
are two points in Minkowski space.
Explicitly we have
where  is the Heaviside step function.
is the Heaviside step function.
See also
External links
- Weisstein, Eric W., "d'Alembertian" from MathWorld.